Rescaling Transformations

Rescaling transformations provide mathematically precise control over scalar field output ranges through univariate functions.

Given a scalar field $F^i:{\mathbb{R}}^{m\times n}\to {\mathbb{R}}^m$, a rescaling transformation produces a new field:

$$G^i(\mathbf{x})=\eta (F^i(\mathbf{x}))$$

where $\eta :\mathbb{R}\to \mathbb{R}$ is a univariate function, applied element-wise to the field. This composition preserves the geometric structure of the original field while transforming scalar values according to the chosen function $\eta$.

Function Classes

1. Hyperbolic Tangent Family: Standard and scaled tanh functions
2. Logistic (Sigmoid) Family: Standard and scaled sigmoid functions
3. Arctangent Family: Standard and scaled arctan functions
4. Error Function: Gaussian-like transition with erf approximation
5. Soft Clipping: Linear preservation with asymptotic bounds

Properties of Rescaling

Rescaling transformations maintain several important geometric properties:

1. Isosurface Preservation: If ${\mathcal{S}}_c=\{\mathbf{x}:F^i(\mathbf{x})=c\}$ is an isosurface of $F^i$, then the transformed field has corresponding isosurfaces at $\eta (c)$.
2. Monotonicity: For strictly monotonic $\eta$, the relative ordering of field values is preserved.
3. Bounded Output: Many rescaling functions map $\mathbb{R}$ to bounded intervals, providing guaranteed output ranges.
4. Differentiability: Most rescaling functions are smooth $C^{\infty }$ functions, meaning they have continuous derivatives of all orders. This property is crucial for:
   • Gradient-based optimization
   • Surface normal computation
   • Analytical ray-surface intersection

Rescaling for Ray Cast Stability

Rescaling transformations are crucial for ensuring numerical stability in ray casting operations. Consider the contrived construction:

$f(\lambda )$ is a univariate function, representing the scalar field's value along a single ray. Ray casting is the process of finding a root of $f(\lambda )=0$ to within a tolerance $ϵ$.

The floating point number line is not uniformly distributed. The difference between two adjacent numbers that are representable increases as the numbers get larger. This means for high-gradient fields (e.g., large shapes where, at the isosurface, the field is changing rapidly), there is no representable value of $\lambda$ that can satisfy the tolerance $ϵ$. This is shown in the first inset below.

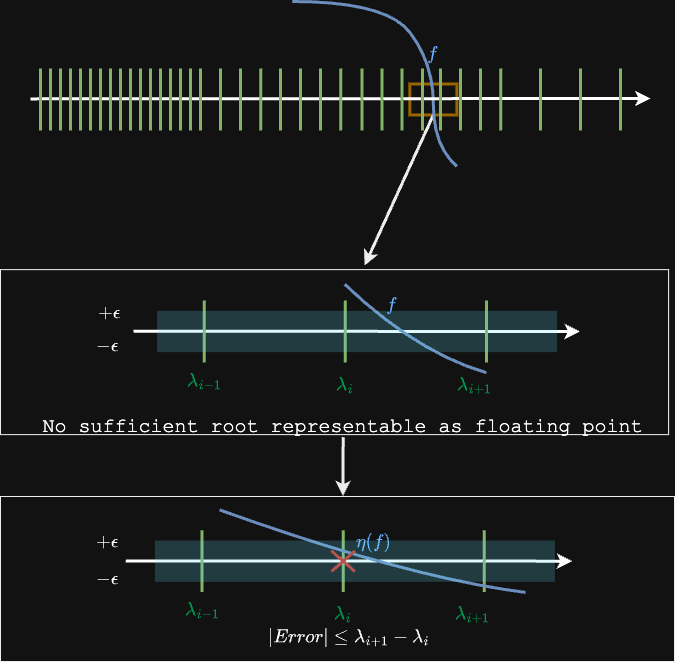
To rectify this, we use our rescaling transformations to map the field values to a closed interval. This has the effect of vertically compressing the field. It is shown in the second inset above.

This method ensures that at least one value of $\lambda$ exists that satisfies the tolerance $ϵ$, and for continuous fields, the converged value of $\lambda$ is at most one floating point number away from the true root.

References

For foundational mathematical techniques:

• Abramowitz & Stegun Handbook of Mathematical Functions (1964) 12
• Press et al. Numerical Recipes (2007) 13
• Boyd & Vandenberghe Convex Optimization (2004) 14