Marching Cubes Algorithm

Marching cubes is one of the most widely used algorithms for isosurface extraction, producing a triangular mesh approximation of the isosurface 1.

In crater.rs, the algorithm is implemented with GPU acceleration using the Burn tensor computation library, making it highly efficient even for large grids.

Overview

The marching cubes algorithm converts implicit surfaces (represented by scalar fields) into explicit triangular meshes. This is essential for visualization, 3D printing, and further geometric processing.

Why Marching Cubes?

Universal: Works with any scalar field function
Robust: Handles complex topologies automatically
Efficient: GPU-accelerated implementation
Widely Supported: Standard mesh format output (STL, VTK)

Core Algorithm Steps

Grid Construction: Create a voxel grid $X_{j}^{i}$ with $(n_{x} + 1) \times (n_{y} + 1) \times (n_{z} + 1)$ vertices within a bounding box
Field Evaluation: Evaluate the scalar field at each grid vertex: $F^{i} (X_{j}^{i})$ for all vertices
Voxel Processing: For each voxel in the grid:
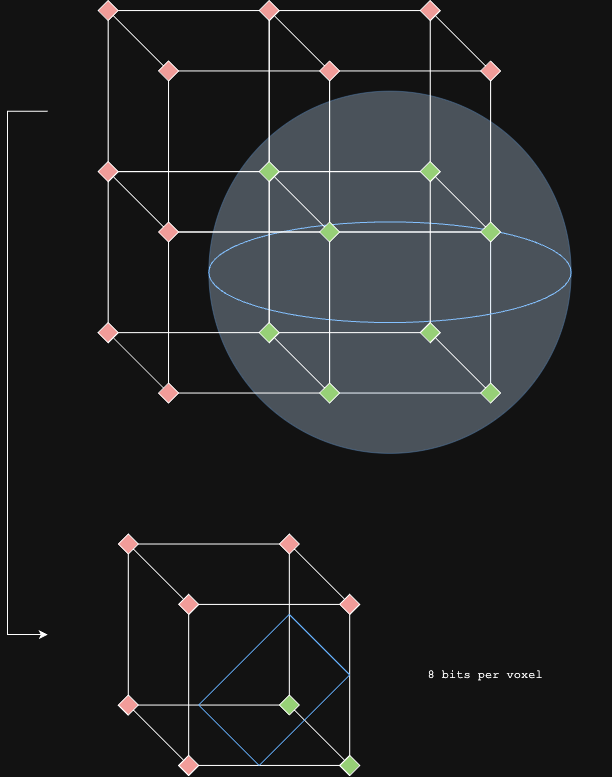
- Determine which of the 8 corners are inside or outside the isosurface
- Compute the 8-bit cube index (0-255) based on corner classifications. This can be done with a tensor convolution over $F^{i} (X_{j}^{i})$ reshaped to $(1, n_{x} + 1, n_{y} + 1, n_{z} + 1)$ with a kernel of shape $(8, 1, 2, 2, 2)$ and stride 1.
- If cube index indicates the isosurface intersects the voxel:
  - Lookup triangle configuration in edge table
  - For each edge intersected by the isosurface:
    - Interpolate vertices to find the exact intersection point
  - Construct triangles using the interpolated intersection points
Mesh Assembly: Collect all triangles into a single mesh

Mathematical Foundation

Cube Classification

Each voxel has 8 corners, labeled 0-7. For each corner $k$ , we evaluate:

If $F (cor n e r_{k}) < 0$ : corner is inside (bit = 1)
If $F (cor n e r_{k}) \geq 0$ : corner is outside (bit = 0)

The cube index is computed as: $index = k = 0 \sum 7 bit_{k} \times 2^{k}$

This gives 256 possible configurations (0-255).

Marching Cubes Configurations

Edge Interpolation

When the isosurface crosses an edge between vertices $v_{1}$ and $v_{2}$ with field values $f_{1}$ and $f_{2}$ , the intersection point is:

$p = v_{1} + t (v_{2} - v_{1})$

where the interpolation parameter is: $t = \frac{- f _{1}}{f _{2} - f _{1}}$

This assumes linear interpolation along the edge.